If I understand your problem right, you have to find for the formula S1 := [c WU [a WU b]] two satisfiable but non-equivalent formulas phi1 and phi2 such that phi1->!S1 and phi2->!S1 holds, and none of the formulas should be equivalent to S1. It should not be too difficult, let's see.
Let's use the teaching tool to prove the validity of S1, i.e., [c WU [a WU b]]. It will answer that it is not valid by presenting a counterexample where all variables a,b,c are always false. That is what you already have found, i.e., your phi1 is G (!a&!b&!c). We can double check by proving the following implication valid:
(G (!a&!b&!c)) -> ![c WU [a WU b]]
Now, we need to find another such formula. Using the teaching tool again for proving the validity of [c WU [a WU b]] would give us again the same formula, so that is not the way to go.
At this point, you have to ask yourself whether this is the only counterexample to the validity of S1. If it would be so, then !phi1 -> S1 would be valid, since if !phi1 -> S1 is not valid, then there is a path that satisfies !phi1&!S1. That would be different to phi1 but would also satisfy !S1, i.e., it is a second counterexample that you wish to find. So, trying to prove
!(G (!a&!b&!c)) -> [c WU [a WU b]]
yields a counterexample which is a path where b and c are always false and a is alternating with initially being false. Hence, we could use as phi2 the formula
!a & (G( (!a <-> X a) & !b & !c))
I double-checked this by proving the validity of
!a & (G( (!a <-> X a) & !b & !c)) -> ![c WU [a WU b]]
which worked as expected.
Note how we made the tool generate another counterexample which can be done similarly for all kinds of these exercises. This way we found counterexamples phi1 and phi2, and I could continue with finding more like the following ones:
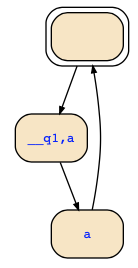
As an alternative, you can consider the omega-automaton that is equivalent to !S1, i.e., the following omega-automaton:
I := !q1
R := (q0<->b|a&next(q0)) & (q1<->q0|c&next(q1))
A := F ((c->q1) & F(a->q0))
As this automaton encodes all counterexamples, you may consider its state transition diagram. Each path that satisfies the acceptance condition is a counterexample that you could use.