Remember that we defined propositional logic on top of the Hilbert base, i.e., negation, conjunction, and disjunction and introduced all other operators as abbreviations. So, you may just use that abbreviation which is how you should read these operators.
Clearly, any equivalent form will also do, so you can use in particular one of the following two:
p⊕q = p&!q | !p&q
p⊕q = (!p|!q)&(p|q)
Which one is better? That depends on your example. Choose a version that minimized branching.
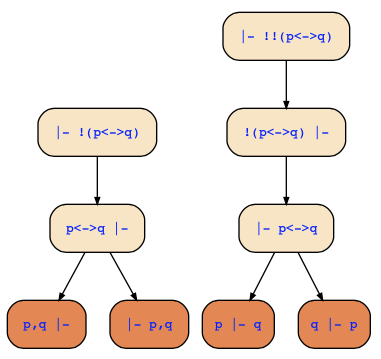
You may also test which rules are used in the teaching tool for the sequent calculus, and if you create proof trees for p⊕q and its negation, you will obtain the following two (internally, there is no ⊕, so it is expanded to a negated equivalence):