[Omega-Automata] Automaton Determinization 2

Question

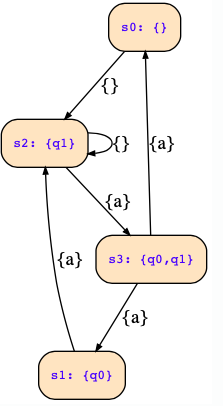
Consider the Co-Büchi automaton with a set of inputs Σ=Σ={{a},{}}, the state variables state=Vstate={q0,q1}, the initial condition φI=!q0&!q1|q0&q1, the acceptance condition  (q0&!q1|q1&!q0), and the following state transition diagram:

The given automaton: 

inputs {a},{}; 

outputs ; 

init 0,3; 

transitions (0,{},,2);(1,{a},,2);(2,{a},,3);(2,{},,2);(3,{a},,0);(3,{a},,1); 

accept 1,2;

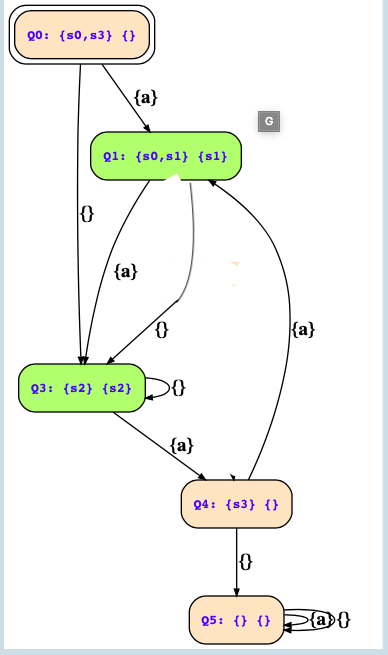
This is my solution which is incorrect as "Q2" is missing with Q_f = {} (Please see the following image for the correct answer as per the tool).

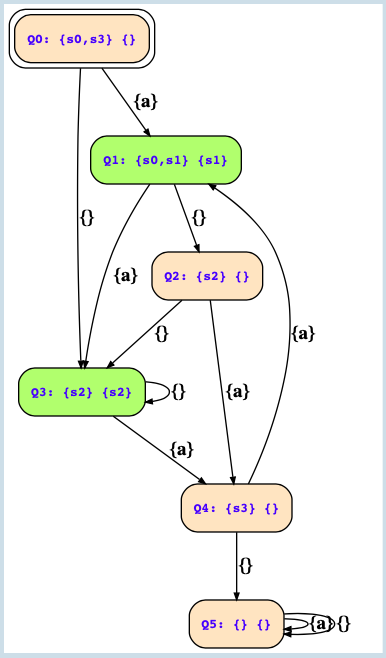
This is the correct solution as per the tool.

My questions:

1. Can someone please explain why was the state "Q2" with (Q,Q_f) = (s₂ , {}) is present in the final solution?

2. The formula in OmegaAutomata slide# 90, states the condition only for the input \sigma, does that \sigma also means an empty input?

3. I am confused with the "Otherwise" condition in the formula on slide#90. Can you please give an example of the "otherwise" condition i.e., when Q_f ≠ {}. Other variants I solved, didn't have duplicate states like in this variant.

Thank you in advance.

Answer 1

Question 1:

You have already found the state Q1 = ({s0;s1},{s1}) in the breakpoint construction and have to compute its successor states for inputs {} and {a}. For input {}, we compute suc∃({s0;s1}) = {s2} and suc∃({s1}) = {}, so that we obtain as successor state for input {} the state Q2 := ({s2},{}).

For input {a}, we compute suc∃({s0;s1}) = {s2} and suc∃({s1}) = {s2} which yields Q3 := ({s2},{s2}) as successor state for input {a}. Don't forget the intersection with the accepting states for the second component which has no effect in the two computations, but has to be considered.

It is just obtained by applying the definition you mentioned.

Question 2: 

The symbol sigma denotes any input letter of the input alphabet. The automaton you consider has the two inputs {} and {a}, and hence, sigma can be any of them. It is just a matter of encoding; instead of {} and {a}, you may also use a boolean variable a which is false and true, or two other symbols a0 and a1. 

Question 3: 

The normal condition is the "otherwise" which means that we compute for both components their successor states. The first case is applied when the second component runs empty (a breakpoint), and we have to restart a new search for an accepting run. The example above is already an example, where we applied the "otherwise" case, isn't it so?

Comments

Now I understand.

computing suc of Q1: ({s0;s1},{s1})
 σ.        Q.      Qf         ( suc∃. (Q) ,     suc∃ (Qf) ∩ F )            [ "otherwise" condition]
{a} : ({s0;s1},{s1})  = ( suc∃({s0;s1}), suc∃({s1}) ∩ F  ) = ( {s2} , {s2} )

 σ.        Q.      Qf         ( suc∃. (Q) ,     suc∃ (Qf) ∩ F )            [ "otherwise" condition]
{} :  ({s0;s1},{s1})  = ( suc∃({s0;s1}), suc∃({s1}) ∩ F )    = ( {s2} , {} )


computing suc Q2: ({s2},{})
 σ.   Q.    Qf       ( suc∃. (Q) ,   suc∃ (Q) ∩ F )            [Qf = {} condition]
{a} : ({s2},{})  =  ( suc∃({s2}), suc∃({s2}) ∩ F  ) = ( {s3} , {} )

 σ.   Q.    Qf       ( suc∃. (Q) ,   suc∃ (Q) ∩ F )            [Qf = {} condition]
{} :   ({s2},{})  =  ( suc∃({s2}), suc∃({s2}) ∩ F  ) = ( {s2} , {s2} )

Thank you for the detailed explanation.