Construction of zdd

Question

can you help with ZDD of above diagram, when i tried my answer (graph of Zdd) is not matching with teaching tool so can you please explain the elemination rule of ZDD for above 

Answer 1

I can read the following formula from the diagram:

    d&c&!b&!a | d&!c&b&!a | !d&c&b&!a | !d&c&!b | !d&!c

Let's first make a Shannon decomposition to make the problem smaller:

    d => c&!b&!a | !c&b&!a
       | c&b&!a | c&!b | !c

and yet another one on c:

    d => c => !b&!a
            | b&!a
       | c => b&!a | !b
            | 1

The ZDD for !b&!a is just the 1-leaf which is seen as follows: A full expansion will be the decision diagram (b=>(a=>0|0)|(a=>0|1)); you may wish to draw that here. Here, we apply the elimination rule to both nodes (a=>0|0) and (a=>0|1) since their high-part is 0; what is left is their low part, i.e., we have (b=>0|1). Again, we apply the elimination rule since the high-part is 0, and what is left is the low part, i.e., 1. 

Next, construct the ZDD for b&!a. The full expansion will be the decision diagram (b=>(a=>0|1)|(a=>0|0)) which is reduced to (b=>1|0).

The ZDD for b&!a | !b is found by the reducing the full expansion (b=>(a=>0|1)|(a=>1|1)) which reduces to (b=>1|(a=>1|1)).

Finally, we need to determine the ZDD for 1 on variables b,a. Again, we consider the full expansion (b=>(a=>1|1)|(a=>1|1)) and see that we cannot eliminate any node. 

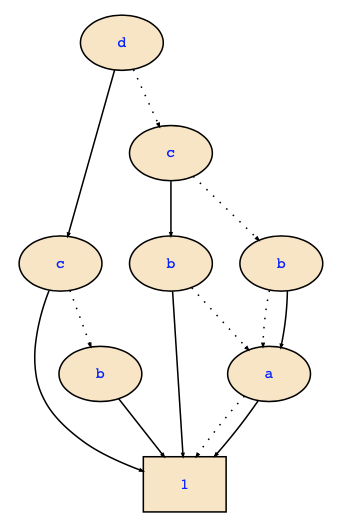
Hence, we now obtain 

    d => c => 1
            | (b=>1|0)
       | c => (b=>1|(a=>1|1))
            | (b=>(a=>1|1)|(a=>1|1))

This corresponds with the following ZDD: