In general, pre∀(Q) contains those states where all transitions (if there are any) point inside Q. Hence, deadend states are inclucded in any set pre∀(Q). We may define pre∀(Q) := {s ∈ S | suc(s) ⊆ Q}.
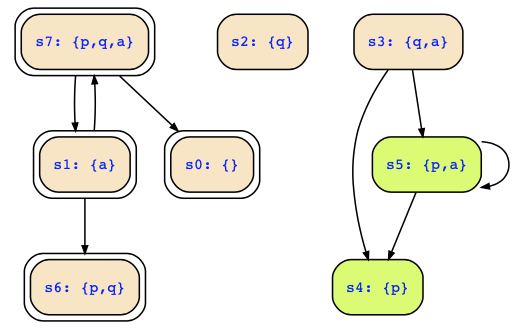
In the first case, which is taken from the exam 2019-08, we compute the universal predecessors of p∧¬q using the transition relation ((p∨q)↔p′)∧(¬p↔q′)∧a and the result mentioned was p∧a. I think that result is wrong and it should rather be p|!a.
Looking at the Kripke structure of the automaton, that means pre∀({s4;s5}) = {s0;s2;s4;s5;s6;s7} = {s0;s2;s4;s6}∪{s5;s7}, which correctly contains the deadend states.
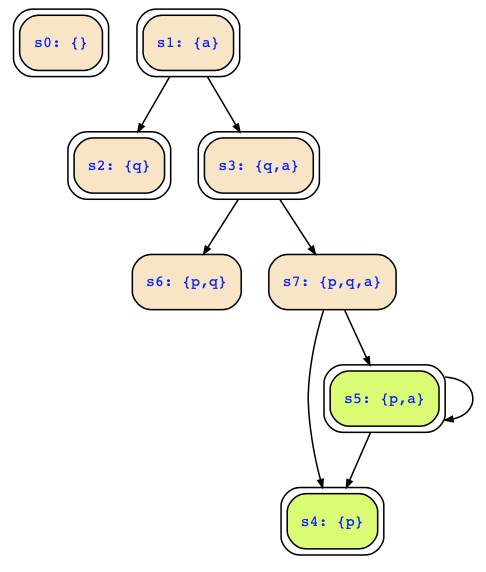
In the second case, which is taken from the exam 2019-02, we also compute the universal predecessors of p ∧ ¬q using the transition relation a∧((p∧q)↔¬p′)∧(q′↔(¬p∧¬q)) and the result is ¬a ∨ a∧¬p∧q ∨ a∧p∧¬q. Looking at the Kripke structure of the automaton, that means pre∀({s4;s5}) = {s0;s2;s3;s4;s5;s6} = {s0;s2;s4;s6}∪{s3;s5}, which also correctly contains the deadend states.