I was sure that somebody will ask this now, and I will have to figure out the difference. Well, here it is:
EG(avXa) cannot be expressed in CTL: Since CTL is closed under negations, and since ¬EG(avXa) is equivalent to AF(¬a⋀X¬a), either both formulas can be expressed in CTL or none of them.
You find on slide 36 of the temporal logic chapter a remark that AF(p⋀Xp) can be expressed in the alternation-free µ-calculus (a µ-calculus formula is given there with a proof). It is also stated that AF(p⋀Xp) cannot be expressed in CTL. The impossibility to express it in CTL is not so difficult to prove, but lengthy; I remember that the proof used induction over the CTL formulas to prove that none of them can be equivalent to AF(p⋀Xp).
Why is EG(avXa) not the same as EG(avEXa)? Equivalently, we may ask also why is AF(a⋀Xa) not equivalent to AF(a⋀AXa)? To see the difference, consider the following Kripke structure:
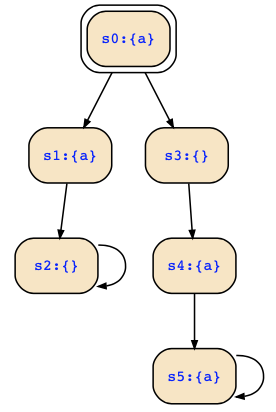
You can see that all paths starting in the initial state s0 satisfy F(a⋀Xa); the path s0s1s2... does so since a⋀Xa holds there immediately, and the path s0s3s4s5... does so since a⋀Xa holds there at time 2, i.e., when we reach state s4. Thus, we have AF(a⋀Xa) in the initial state and therefore this structure satisfies AF(a⋀Xa).
Using our CTL model checking procedure, it is however not difficult to see that
States(a) = {s0;s1;s4;s5}
States(AXa) = {s3;s4;s5}
States(a⋀AXa) = {s4;s5}
States(AF(a⋀AXa)) = {s3;s4;s5}
Hence, AF(a⋀AXa) does not hold in the initial state, and since AF(a⋀Xa) holds there, the structure shows the difference between these two formulas.
If you rather want to see the difference between EG(avXa) and EG(avEXa), then consider EG(¬avX¬a) = ¬AF(a⋀Xa) and EG(¬avEX¬a) = ¬AF(a⋀AXa) and the Kripke structure also shows you their difference.
States(a) = {s0;s1;s4;s5}
States(¬a) = {s2;s3}
States(EX¬a) = {s0;s1;s2}
States(¬avEX¬a) = {s0;s1;s2;s3}
States(EG(¬avEX¬a)) = {s0;s1;s2}
However, there is no path starting in state s0 which would satisfy G(¬avX¬a) which is equivalent to G(a->X¬a). You can easily see this by checking the two initial paths of the Kripke structure.