Short answer: Whether a variable is live or not always refers to a state (=line) of the program. For a basic block, you may therefore distinguish between the variables which are live at the beginning and at the end of the basic block (which are two particular lines of code in that basic block).
Longer answer: In general, a variable is live in a state of a computation path if the value of the variable will be read later on that path. Hence, we know that we should not overwrite that value at the moment, since the value is needed later on.
It is easy to explain liveness on a single computation path. However, compilers have to consider all potential computation paths at compile time. We therefore have to pessimistically assume that all paths are possible even though in reality some are not possible.
For instance, consider the following program
if(a) {
if(a|b) {
S1;
} else {
S2;
}S2 cannot be reached in this program, but the dataflow analysis does still consider it to be reachable (since such cases should not occur). We therefore can distinguish for a variable whether it may/must be live in that there may/must be a path where it is live at this point.
if(a) {
x = 2;
if(a|b) {
y = 3;
} else {
z = x+1;
}The program is first translated to the following internal representation where basic blocks are distinguished by lines:
-----------------------------------
0000 : _t0 := 0 == a
0001 : if _t0 goto 10
-----------------------------------
0002 : x := 2
0003 : _t1 := a | b
0004 : _t2 := 0 == _t1
0005 : if _t2 goto 8
-----------------------------------
0006 : y := 3
0007 : goto 9
-----------------------------------
0008 : z := x + 1
-----------------------------------
0009 : goto 10
-----------------------------------
0010 : end
-----------------------------------See also the CFG of this example below:
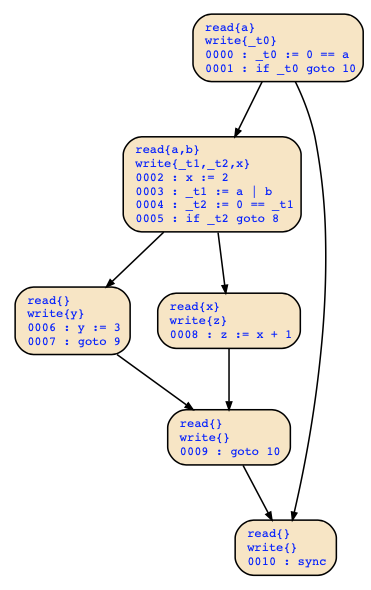
We can now compute the following sets of live variables (MustLive ⊆ MayLive):
0000 : {a} ⊆ {a,b}
0001 : {_t0} ⊆ {_t0,a,b}
0002 : {a,b} ⊆ {a,b}
0003 : {a,b} ⊆ {a,b,x}
0004 : {_t1} ⊆ {_t1,x}
0005 : {_t2} ⊆ {_t2,x}
0006 : {} ⊆ {}
0007 : {} ⊆ {}
0008 : {x} ⊆ {x}
0009 : {} ⊆ {}
0010 : {} ⊆ {}As you can see, variable x becomes may-live after its assignment in line 2, since there is a computation path 2->3->4->5->8->9->10 where it is read later on, namely in line 8. Variable x is however not must-live after its assignment, since there is another path 2->3->4->5->6->7->9->10 where it will not be read later on.
Considering the basic block consisting of lines 2,3,4,5, we can say that x is may-live at the end of the basic block (in line 5), but not at its beginning (in line 2).
Having written this, let me also add that people usually mean may-live if they just talk about liveness of variables. It is an superset of the variables that are really read in the following.