The following formulas are equivalent to each other:
- AG((Fa) ∧ (Fb) ∧ (Fc))
- AGA((Fa) & (Fb) & (Fc))
- AGAFa & AGAFb & AGAFc
However, only the last one is a CTL formula (as required by the exercise).
Moreover, the fourth version mentioned, i.e, AGAF(a&b&c) is not equivalent to the three formulas above. It is equivalent to AGF(a&b&c) and means that on all paths we must have infinitely many points of time where we have a&b&c, while the other version just means that on all paths, we must have infinitely many a,b,c but these may not necessarily occur together (see also the counterexample below).
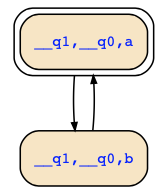
Second, the formulas EGE((Fb) ∧ (Fa)) and EGEF(b&a) are not equivalent for a similar reason: The second formula demands that there there are always points of time where a&b occurs together while the former only demands that a and b occurs. Check the following counterexample where we have E((Fb) ∧ (Fa)) in both states, thus EGE((Fb) ∧ (Fa)), but no state satisfies EF(b&a).