Well, for the grammar
A -> a | BA
B -> a | bB
we obtain
First(A) = {a,b}
First(B) = {a,b}
and
Follow(A) = {$}
Follow(B) = {a,b}
The parse table for a top-down parser would therefore not have unique decisions since the grammar is not LL(1). The LR(0) automaton is as follows:
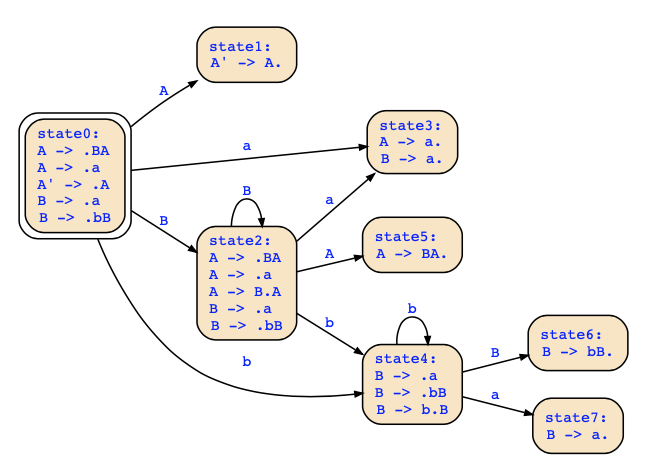
The action table for a LR(0) parser is now determined by the following rules (see slide 178):
- if q_i contains A → α.aβ with a ∈ T, and q_i′ is the state reached in the automaton from q_i reading a, then shift a on the stack and put q_i′ above
- if q_i contains S′ → S. and the input is ε, accept
- if q_i contains B → γ., then reduce with rule B → γ
This yields the following action table:
state | a | b | $ | A | B |
q0 | S(3) | S(4) | | G(1) | G(2) |
q1 | | | A | | |
q2 | S(3) | S(4) | | G(5) | G(2) |
q3 | R(B->a) | R(B->a) | R(A->a) | | |
q4 | S(7) | S(4) | | | G(6) |
q5 | | | R(A->BA) | | |
q6 | R(B->bB) | R(B->bB) | | | |
q7 | R(B->a) | R(B->a) | | | |
For instance, in state q0, we have the rule A ->.a which leads to a shift action for a that leads to the new state q3, and we we have the rule B -> .bB that leads to the shift action for b that leads to state q4. There is a reduce/reduce conflict in state 3 since we could reduce with A-> a. and also with B->a. as well.
Therefore, the grammar is not a LR(0) grammar and we need to construct the SLR(1) action table. Here the third rule above becomes
and this resolves the reduce/reduce conflict.