Even though I should not post the entire solution, I will do so here since there are quite some confusions about this kind of exercise. Using the state encoding s0:{}, s1:{p}, s2:{q}, s3:{p,q}, the FSM has the following states (as can be seen in the state transition diagram you posted):
- initial states: {s1,s3}
- reachable states: {s1,s3}
- dead(end) states: {s2}
- finally dead(end) states: {s2}
The corresponding Kripke structure looks as follows:
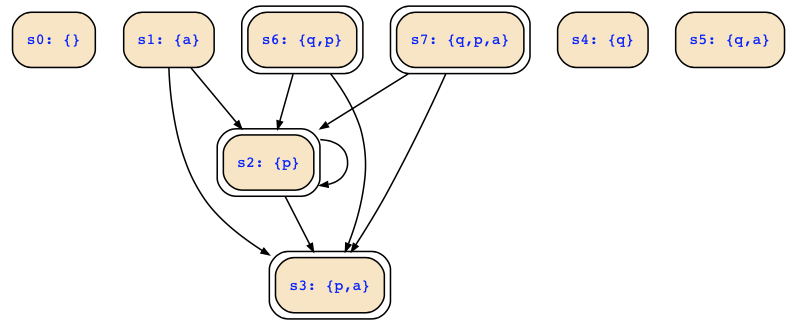
and has
- initial states: {s2,s3,s6,s7}
- reachable states: {s2,s3,s6,s7}
- dead(end) states: {s0,s3,s4,s5}
- finally dead(end) states: {s0,s3,s4,s5}
Part 1a):
It asks for initial states, but actually it means the initial states that are not finally dead states. Hence, these are states {s2,s3,s6,s7}\{s0,s3,s4,s5} = {s2,s6,s7} represented by p&!q&!a | p&q&!a | p&q&a or simpler p&!a | p&q&a
Part 1b):
Again, it asks for reachable states, but actually means reachable states that are not finally dead states. Hence, these are states {s2,s3,s6,s7}\{s0,s3,s4,s5} = {s2,s6,s7} which is the same set of states as above.
Part 1c):
The (finally) dead states are {s0,s3,s4,s5} where only state s3 has incoming transitions. To remove them, we modify the transition relation as follows:
(!p&!q& a & !next(q) & next(p) |
p& q& !next(q) & next(p) |
p&!q&!a & !next(q) & next(p)
) & !(next(p)&!next(q)& next(a))
which is now the following state transition diagram:
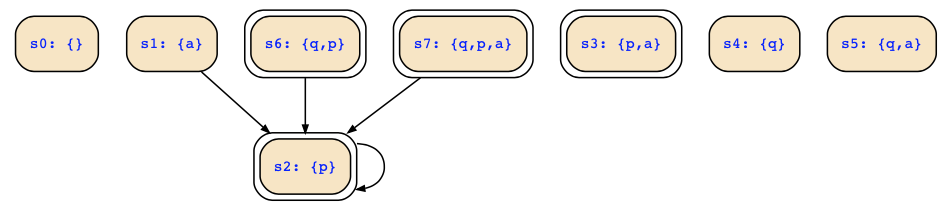
If you don't like to inspect the state transition diagram, you may also check that the deadend states are encoded as
s0 : !p&!q&!a
s3 : p&!q& a
s4 : !p& q&!a
s5 : !p& q& a
so that the set of deadend states is represented by !p&!q&!a | p&!q& a | !p& q or even simpler by !p&!a|p&!q&a|!p&q. The transitions that do not lead to deadend states are therefore R&!next(deadend) which is
(!p&!q& a & !next(q) & next(p) |
p& q& !next(q) & next(p) |
p&!q&!a & !next(q) & next(p)
) & !(!next(p)&!next(a)|next(p)&!next(q)&next(a)|!next(p)&next(q))
Part 1d):
Now we shall remove the transitions from/to unreachable states, and I assume that again, only reachable states without the deadend states is meant here. The reachable states are {s2,s3,s6,s7} and the finally dead states are {s0,s3,s4,s5} so that we have {s2,s3,s6,s7}\{s0,s3,s4,s5} = {s2,s6,s7}. These states are encoded as follows:
s2: p&!q&!a
s6: p& q&!a
s7: p& q& a
So that {s2,s6,s7} is encoded by p&!q&!a | p& q&!a | p& q& a or equivalently by p&q|p&!a. To allow only transitions among these states, we replace the transition relation as follows:
(!p&!q& a & !next(q) & next(p) |
p& q& !next(q) & next(p) |
p&!q&!a & !next(q) & next(p)
)
& (p&q|p&!a)
& (next(p)&next(q)|next(p)&!next(a))This yields the following state transition diagram:
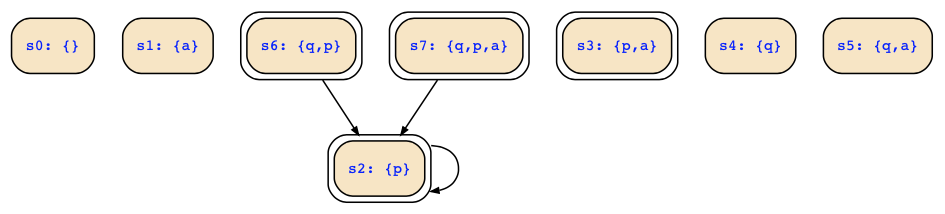
Hence, you can also simplify the transition relation to
(p&q | p&!q&!a) & !next(q) & next(p)& !next(a)