LTL Equivalence

Question

Below is the question from the online exercies "LTL Equivalence".

   S1=X a -> G c
   S2=F a -> X c

I tried with the tool and it says both S1->S2 and S2->S1 are invalid.

I also failed to construct a Kripke structure to find a counter example that satifies one but not other. I am not sure if I am using the tool in a correct way. However, I am more interested to find the solution in a manual way.

Could you please explain how to solve it?

Thanks!

Answer 1

You already found solutions, but were too confused to see them: It is fine that both S1->S2 and S2->S1 are invalid. Then, we can generate a path where S1&!S2 holds, and another path where !S1&S2 holds.

Checking validity of (X a -> G c) -> (F a -> X c) yields a counterexample with two states where variable "a" is alternatingly true and false:

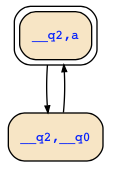
On the unique initial path, X a is false, so X a -> G c is true, and F a is true, but X c is false, so that F a -> X c is false. That is fine, we have a structure that satisfies S1 := X a -> G c but not S2 := F a -> X c.

The other way around, checking validity of (F a -> X c)->(X a -> G c) yields a counterexample with two states where variable "a" is alternatingly true and false:

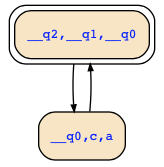
The initial path satisfies F a, X a, X c, thus F a -> X c, and it does not satisfy G c, and therefore also not X a -> G c. Hence, S2 is satisfied here, but S1 is not satisfied.

Comments

Is there a way of using tool to draw Kripke structures for the entered LTL or CTL fomulas? For example, I want to see the some Kripke structures for "EGEFa".

And I know that the results are not conanical, and there are multiple solutions. But is it possible that the tools gives us few examples?

If we cannot use the tool is there any other way? (This helps to practice more and to self-evaluate)

Thanks!

---

For LTL, there is a tool and it also draws the Kripke structure which is just one path with a single loop since that is sufficient for LTL.

For CTL and even CTL*, things are more difficult. In particular, for CTL*, the complexity is doubly exponential which becomes prohibitive in many cases. Still, there is an experimental tool that you can test: https://es.cs.uni-kl.de/tools/teaching/PreStructures.html