For a given formula φ, we may first compute its cofactors [φ]_x^1 and [φ]_x^0 on a variable x by replacing every occurrence of x in φ by 1 for the positive cofactor and by 0 for the negative cofactor. The positive Davio decomposition is then defined as φ = [φ]_x^0 ⊕ x & ([φ]_x^0 ⊕ [φ]_x^1) where the two decomposed parts [φ]_x^0 and [φ]_x^0 ⊕ [φ]_x^1 are sufficient to reconstruct φ.
In case of the formula a&c|a&!b&!c, we therefore obtain cofactors on c as
- [a&c|a&!b&!c]^1_c = a&1|a&!b&!1 = a
- [a&c|a&!b&!c]^0_c = a&0|a&!b&!0 = a&!b
and based on this, the positive Davio decomposition (a&!b) ⊕ c & (a⊕a&!b). Let me note here that a⊕a&!b is equivalent to a&b even though that simplification is not required in the following, but it simplifies matters.
I assume that it should be continued for the variables b and a so that a FDD or the Reed-Muller form will be obtained. So, we continue with decomposing a&!b:
- [a&!b]_b^1 = a&!1 = 0
- [a&!b]_b^0 = a&!0 = a
to decompose it as a&!b = a ⊕ b & (a⊕0) = a ⊕ b&a.
And for a&b (or equivalently a⊕a&!b), we obtain:
- [a&b]_b^1 = a&1 = a
- [a&b]_b^0 = a&0 = 0
to decompose it as a&b = 0 ⊕ b & (0⊕a) = b&a.
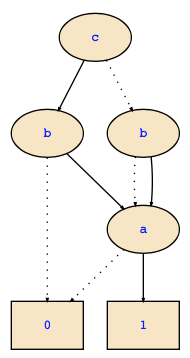
Putting things together we obtain the following "FDD":
a&c|a&!b&!c
= (a&!b) ⊕ c & (a⊕a&!b)
= (a ⊕ b&a) ⊕ c & (0 ⊕ b & (0⊕a))
which we may further derive into a Reed-Muller form:
= a ⊕ b&a ⊕ c&b&a
The FDD is shown below: