Attractors are computed as explained on slide 150, and some or their properties are also mentioned there. Hence, your formulas for the attractors are correct. For this reason, computing attractors is done by µ-calculus model checking.
About your second question, win1'={s0, s1, s2, s3} is not a path, but the set of states where player 1 has a winning strategy. We thereby consider the game on page 161 and yes, the highest rank of the four states is the rank of state s1 which is 16 and that number is even. However, state s1 cannot be visited infinitely often. There are just two paths, the one where we always loop in s0 such that the highest rank would be 3, and the other path is s3 s1 (s2 s4)^omega where the states visited infinitely often are s2 and s3 and thus the highest rank visited infinitely often is 5 which is also odd, so that player 1 also wins that play.
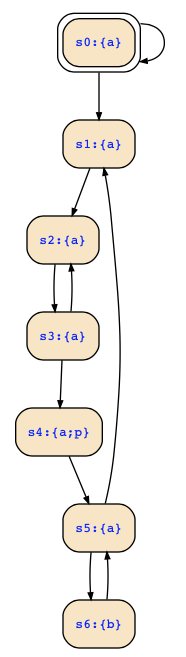
For the game on page 160 that you consider, we have to compute attr1({s4}) and later then also attr0(win0') for the second recursive call. These are computed in the game that is considered as a Kripke structure with the above fixpoints. Hence, in detail, the computation is as follows:
µx.(p ∨ a∧<>φ ∨ b∧[]φ):
〖p〗= {s4}
〖q〗= {s5;s6}
〖a〗= {s0;s1;s2;s3;s4;s5}
〖b〗= {s6}
step 0 : x = {}
〖x〗= {}
〖<> x〗 = {}
〖[] x〗 = {}
〖a & [] x〗 = {}
〖b & <> x〗 = {}
〖p | a & [] x | b & <> x〗 = {s4}
step 1 : x = {s4}
〖x〗= {s4}
〖<> x〗 = {s3}
〖[] x〗 = {}
〖a & [] x〗 = {}
〖b & <> x〗 = {}
〖p | a & [] x | b & <> x〗 = {s4}
fixpoint reached!and the second attractor:
computing states of mu x:bool. (q | a & <> x | b & [] x)
step 0 : x = {}
〖x〗= {}
〖<> x〗 = {}
〖a & <> x〗 = {}
〖[] x〗 = {}
〖b & [] x〗 = {}
〖q | a & <> x | b & [] x〗 = {s5;s6}
step 1 : x = {s5;s6}
〖x〗= {s5;s6}
〖<> x〗 = {s4;s5;s6}
〖a & <> x〗 = {s4;s5}
〖[] x〗 = {s4;s6}
〖b & [] x〗 = {s6}
〖q | a & <> x | b & [] x〗 = {s4;s5;s6}
step 2 : x = {s4;s5;s6}
〖x〗= {s4;s5;s6}
〖<> x〗 = {s3;s4;s5;s6}
〖a & <> x〗 = {s3;s4;s5}
〖[] x〗 = {s4;s6}
〖b & [] x〗 = {s6}
〖q | a & <> x | b & [] x〗 = {s3;s4;s5;s6}
step 3 : x = {s3;s4;s5;s6}
〖x〗= {s3;s4;s5;s6}
〖<> x〗 = {s2;s3;s4;s5;s6}
〖a & <> x〗 = {s2;s3;s4;s5}
〖[] x〗 = {s2;s4;s6}
〖b & [] x〗 = {s6}
〖q | a & <> x | b & [] x〗 = {s2;s3;s4;s5;s6}
step 4 : x = {s2;s3;s4;s5;s6}
〖x〗= {s2;s3;s4;s5;s6}
〖<> x〗 = {s1;s2;s3;s4;s5;s6}
〖a & <> x〗 = {s1;s2;s3;s4;s5}
〖[] x〗 = {s1;s2;s3;s4;s6}
〖b & [] x〗 = {s6}
〖q | a & <> x | b & [] x〗 = {s1;s2;s3;s4;s5;s6}
step 5 : x = {s1;s2;s3;s4;s5;s6}
〖x〗= {s1;s2;s3;s4;s5;s6}
〖<> x〗 = {s0;s1;s2;s3;s4;s5;s6}
〖a & <> x〗 = {s0;s1;s2;s3;s4;s5}
〖[] x〗 = {s1;s2;s3;s4;s5;s6}
〖b & [] x〗 = {s6}
〖q | a & <> x | b & [] x〗 = {s0;s1;s2;s3;s4;s5;s6}
step 6 : x = {s0;s1;s2;s3;s4;s5;s6}
〖x〗= {s0;s1;s2;s3;s4;s5;s6}
〖<> x〗 = {s0;s1;s2;s3;s4;s5;s6}
〖a & <> x〗 = {s0;s1;s2;s3;s4;s5}
〖[] x〗 = {s0;s1;s2;s3;s4;s5;s6}
〖b & [] x〗 = {s6}
〖q | a & <> x | b & [] x〗 = {s0;s1;s2;s3;s4;s5;s6}
fixpoint reached!