To get the transitions which are encoded by a symbolic transition relation like (p <-> b|a&next(p)) & (q<->p&next(q)), we have to list all satisfying assignments of that propositional logic formula. As usual, that can be done in many ways, e.g., using Shannon composition, computing a DNF or a BDD, using the sequent calculus, or some other method.
My recommendation is to make a Shannon decomposition on the current state variables. For the mentioned example, we get
(p <-> b|a&next(p)) & (q<->p&next(q))
= (p ? (b|a&next(p)) & (q<->next(q))
: !(b|a&next(p)) & !q )
= (p ? (q ? (b|a&next(p)) & next(q)
: (b|a&next(p)) & !next(q) )
: (q ? 0
: !(b|a&next(p)) ))
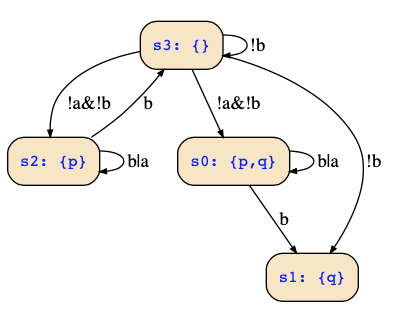
So, we see that from state {q}, there are no outgoing transitions, and all transitions from state {p} are encoded by !(b|a&next(p)), i.e., !b&!a | !b&!next(p)). To get all the transitions, we take the transition relations of the particular states, and further decompose by variables a and b:
(p ? (q ? (b ? next(q) : a & next(p) & next(q) )
: (b ? !next(q) : a & next(p) & !next(q) ) )
: (q ? false
: !b&(!a|!next(p)) ))
Now consider the state {p=0;q=0}, where we get the transitions !b&(!a|!next(p)), or the equivalent form !(b|a) | !(b|next(p)) you got. The satisfying assignments are seen by converting this to a DNF which is !b&!a | !b&!next(p). Hence, with input !b&!a, any state can be reached, and with input !b (and arbitrary a), we can reach the states where p is false, i.e., {} and {q}.
In total, you should get the following transitions: