How to generate Kripke structure containing state names with the online tool?

Question

How can I use the online tool so that the states of the Kripke structure don't contain state names like "s2" (see image below) but instead the actual states "p", "q" and so on as to be seen in the answer to this question?

Further how can I choose whether I want to generate a Kripke structure with deadends or without deadends?

Comments

Which Tool did you use to construct this Kripke Structure?

---

I used the Automata Construction tool: https://es.cs.uni-kl.de/tools/teaching/Automata.html

But I also tried the Symbolic Representation to no avail so far.

---

The tool  https://es.cs.uni-kl.de/tools/teaching/Automata.html is useful when to compute the Kripke structure of an explicitly given automaton, but it is not good when the automaton is given in a symbolic representation. In the latter case you need https://es.cs.uni-kl.de/tools/teaching/SymbolicStateTrans.html.

Answer 1

Hmh, I don't know exactly what you want, but let me explain what often needs to be done when dealing with symbolic representations of FSMs and Kripke structures. 

Assume you are given a FSM with state variables p,q and input/output variables a,o and the following initial states and state transitions:

    I = !(p&q)
    R =  !((q&o->next(q))->next(p)|p|a)

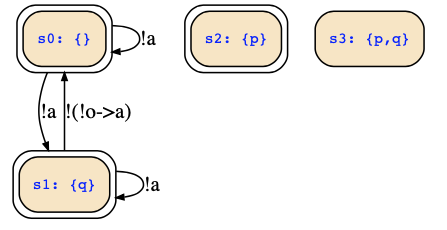
You can use https://es.cs.uni-kl.de/tools/teaching/SymbolicStateTrans.html with the following inputs to generate the state transition diagram of the FSM:

    state variables     : p,q  
    input variables     : a,o
    initial states      : !(p&q)
    transition relation : !((q&o->next(q))->next(p)|p|a)
    state set           : false

The state set given does actually not matter for our purpose here. We come to that later. The tool will generate the FSM which looks as follows:

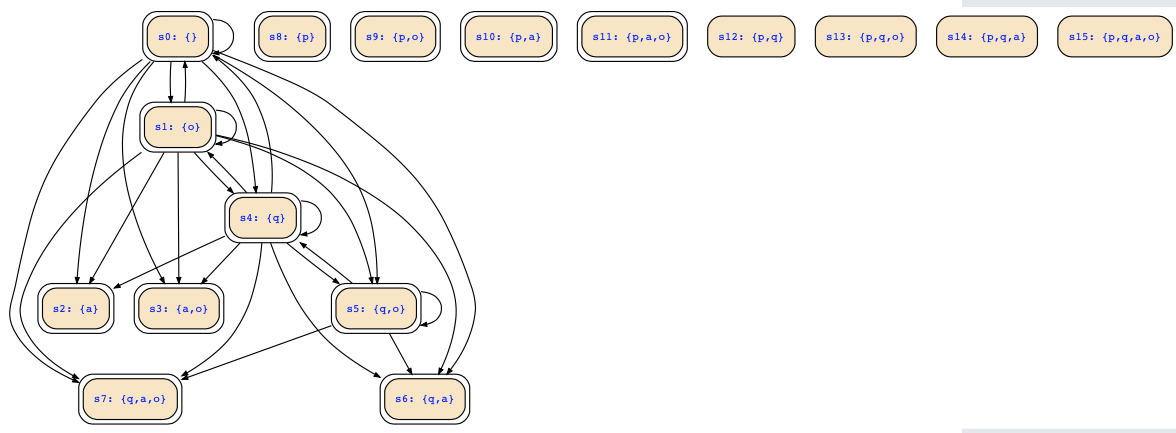
If you now want to see the Kripke structure, you just have to change the input as follows:

    state variables     : p,q,a,o
    input variables     : 
    initial states      : !(p&q)
    transition relation : !((q&o->next(q))->next(p)|p|a)
    state set           : false

This means that there are no input variables and the former input/output variables are now state variables that will form the labels for the states. The rest remains the same.The tool will now show you the Kripke structure, but that will contain deadend states:

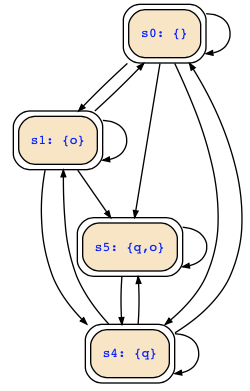
If you want to get rid of the transitions to deadend states, you first need to describe them in propositional logic. The deadend states are those states that satisfy pre∀(false), so you let the tool now compute the universal predecessors of false, and it will compute them in symbolic form as (p|a)&(!(q&o)->p|a) which is equivalent to p|a. You now have to state that you don't want to have transitions to these states, so you modify the transition relation as follows:

    !((q&o->next(q))->next(p)|p|a) & !(next(p)|next(a))

In general, that may create new deadend states that you can also compute and cut off by adding another conjunct ot the transition relation. In the above example, this does however not happen, and you obtain the following:

Does that approach to the answer of your question?

Comments

Yes, that answers my question. Thanks for that great answer.

Answer 2

I think that you can use the Symbolic Representation Tool to generate a Kripke Structure of a FSM:

My FSM is this:

which can be used as a input like this: (It is important to use the input variables of the FSM as state variables now, the "state set" does not matter but is required as an input):

Above you can see the solution. Remember to remove initial state property from dead-ends. The graph also displays dead-ends just like you asked.