converting given automaton to kripke structure

Question

when converting a given automaton : (inputs a1,a2;outputs o1,o2;init 1;transitions (0,{a2},{o2},3);(2,{a2},{o2},3); (3,{a2},{o2},3);(1,{a1},{o2},3);(1,{a2},{o1},3);(1,{a1},{o1},3);(1,{a2},{o2},3);) to a kripke structure, i get the a dead end with the following: s1:{a1,s3} s2: {a2,s3}. does this mean !p&!q&a | !p&!q&!a ?

where o1 represents {o}, o2 represents {}, a1 represents {a} and a2 represents {}.

Attached below is the kripke structure

Comments

I'm not quite sure which of the many deadend state you are talking about.

---

I updated the question with a diagram, from the diagram i believe there are only 2 deadends (states with no successors): , s1:{a1,s3} s2: {a2,s3}. My question is does the deadend s1 represent !p&!q&a ?

---

Tip: Set the width of the image to 100%

---

i've updated the picture width

---

I'm confused. If you look at the FSM, there should be much more states. For example, the ones associated to s0 with other signals than {a2}/{o2}. Similarly, I don't see the s3-self-loop in the Kripke structure …

---

I tried to generate the kripke structure from the fsm transitions using the automata to kripke tool. Is there a particular tool I can use to directly transform the fsm to a kripke structure or do I have to do it manually?

---

For symbolic Kripke structures, I suggest what has been suggested here: https://q2a.cs.uni-kl.de/761/generate-kripke-structure-containing-state-names-with-online

Answer 1

Looking at your input, I find that you listed (1,{a1},{o2},3) twice. So, I removed it and sorted the transitions but I don't think that this made trouble. Then, I realized that you are mixing up symbolic and explicit representations which makes the tools going wrong. 

What you want to give as input is an explicit representation of the automaton. You want two inputs a1 and a2 and two output o1 and o2. Thus, you should not use the sets for the input and output symbols and instead your automaton should be described as follows:

    inputs a1,a2;
    outputs o1,o2;
    init 1;
    transitions 
        (0,a2,o2,3);
        (1,a1,o1,3);
        (1,a1,o2,3);
        (1,a2,o1,3);
        (1,a2,o2,3);
        (2,a2,o2,3); 
        (3,a2,o2,3);

This will produce the same automaton as you had, just without the brackets:

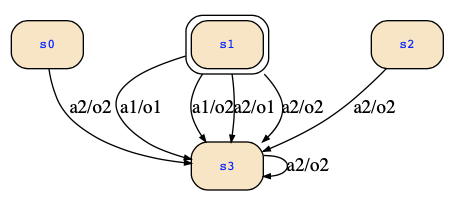
As you can see, states 0,2 and 3 cannot react to input a1 and can only produce output o2 for the input a2. The tool also prints that information 

    0 transitions for state 3 and input a1
    0 transitions for state 2 and input a1
    2 transitions for state 1 and input a2
    2 transitions for state 1 and input a1
    0 transitions for state 0 and input a1

This will lead to deadend states for these states in the Kripke structure. The tool https://es.cs.uni-kl.de/tools/teaching/Automata.html only prints the states that belong to transitions (either incoming or outgoing) since it creates for the given transitions of the FSM corresponding transitions of the Kripke structure. The correct figure is now the following:

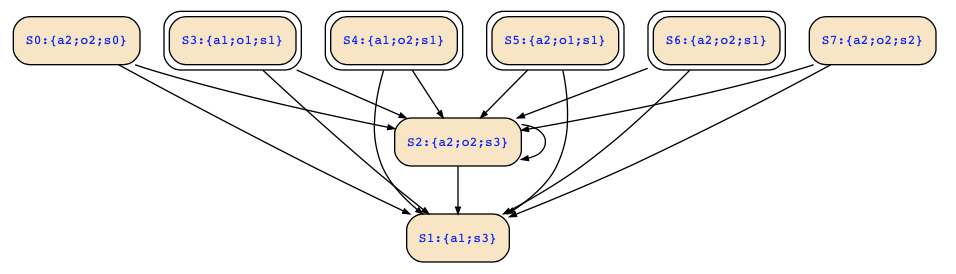
Now, you do not see the all deadend states you would like to see, but just because this tool doesn't show them (as I wrote above, it just expands the FSM transitions), but it listed them at first as well as the tool did. 

If you consider a symbolic representation with states 0,1,2,3 encoded as !p&!q,!p&q,p&!q and p&q, respectively: 

        !p&!q & !a & !o & next(p) & next(q) |
        !p& q &           next(p) & next(q) |
         p&!q & !a & !o & next(p) & next(q) |
         p& q & !a & !o & next(p) & next(q) 

you can also use the tool https://es.cs.uni-kl.de/tools/teaching/SymbolicStateTrans.html and that also computes as pre∀(false) the deadend states as 

!(!o&!a&p&q|!o&!a&p&!q|q&!p|!o&!a&!p&!q) 

which is equivalent to p&a|p&o|!q&a|!q&o which are the following nine states:

 !p&!q&!a& o |
  p& q& a& o |
  p& q& a&!o |
  p& q&!a& o |
  p&!q& a& o |
  p&!q& a&!o |
  p&!q&!a& o |
 !p&!q& a& o |
 !p&!q& a&!o

If you now let the same tool print the Kripke structure, you will see them all: