You have an FSM with state variables p,q and input variable a and initial states p&q|!p&!q and the following transition relation
R = p& q&!next(q)&next(p)
| p&!a&!q&!next(q)&next(p)
| q&!a&!p&!next(q)&next(p)Remark: It would be nice of you if you would type that in instead of making a screen shot where we have to type in the formulas.
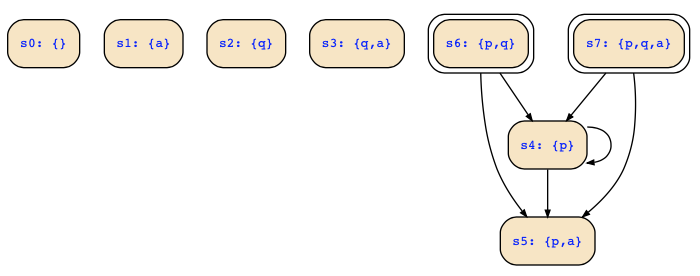
The FSM corresponds with the following Kripke structure:
The deadend states are computed as pre∀(false) which is !q&a|!p&a|!p&!q which can be written in full DNF as
!p&!q&!a | !p&!q&a | !p&q&a | p&!q&a
Hence, we have four deadend states that you can also directly see in the above figure. You also have written a fifth one p&!q&a which is however the same as the fourth.
Moreover, there is an unreachable state s2:{q} that we also have to eliminate. Thus, we replace the above transition relation with
I1 = (p&q|!p&!q) & !(!p&!q&!a | !p&!q&a | !p&q&a | p&!q&a)
R1 = R & !(!p&q&!a) & !(!next(q)&next(a)|!next(p)&next(a)|!next(p)&!next(q))
which is equivalent to
I1 = p&q&a | p&q&!a
R1 = p&!q&!a&next(p)&!next(q)&!next(a)
| p& q& a&next(p)&!next(q)&!next(a)
| p& q&!a&next(p)&!next(q)&!next(a)
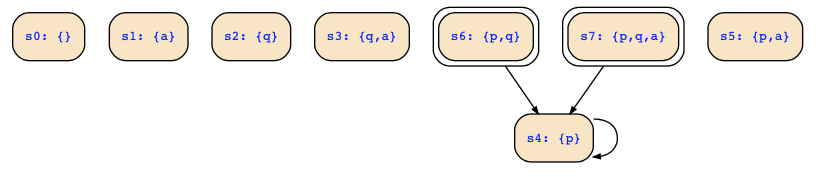
This structure looks now as follows:
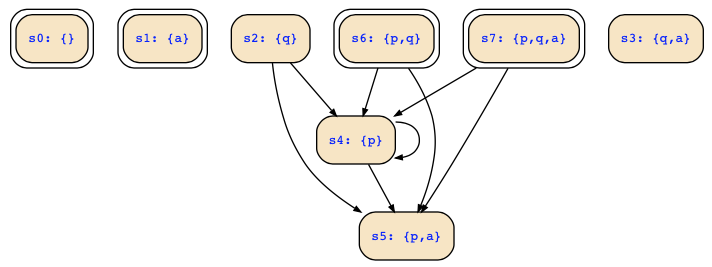
Your transition relation !a&p&q&next(p)&!next(q) | a&p&q&next(p)&!next(q) | !a&p&!q&next(p)&!next(q) produces however the following transitions, and you can now see where you go wrong: