Type of Automaton

Question

Question from exercise:

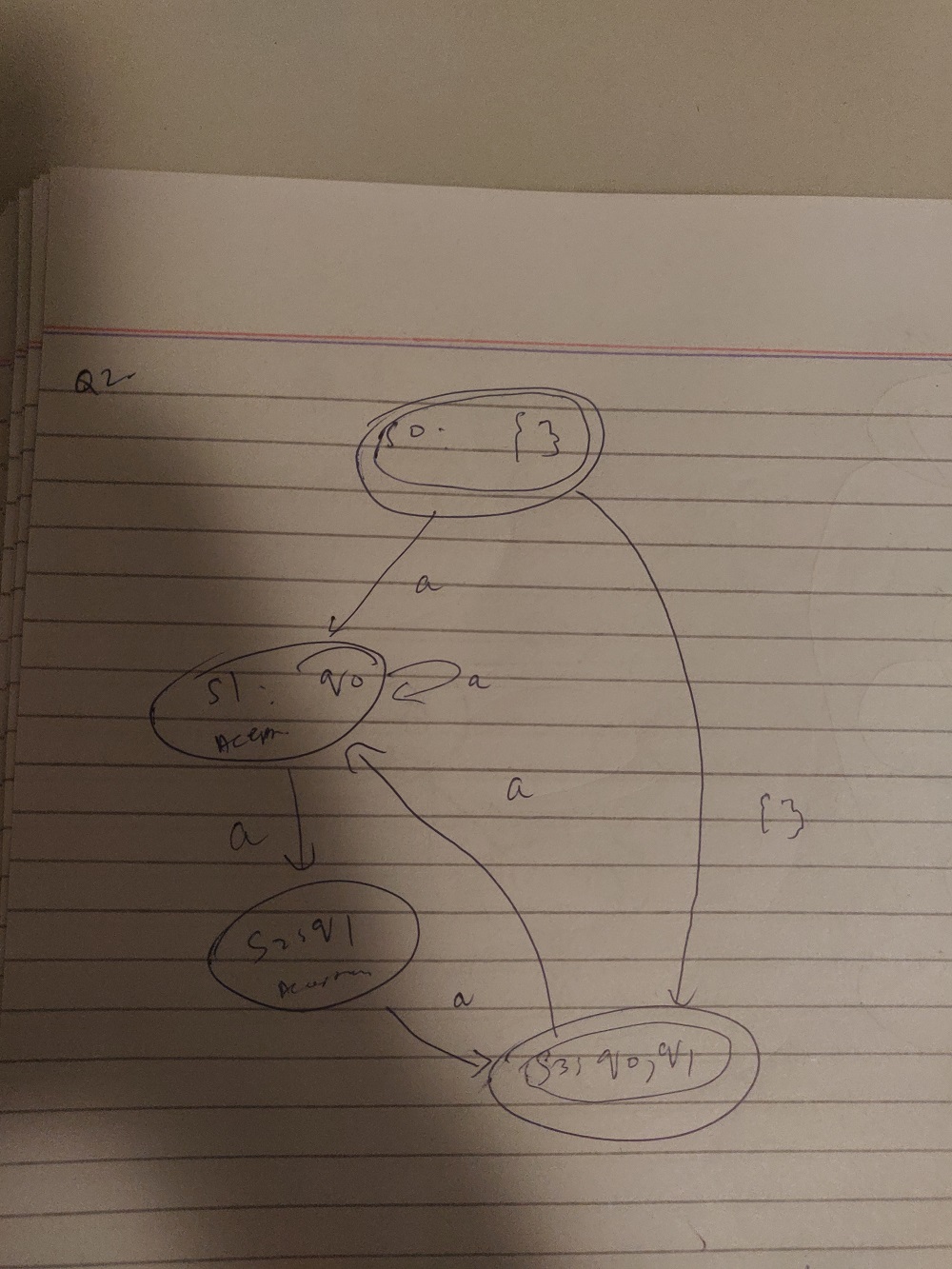
My construction as first step:

My Final construction:

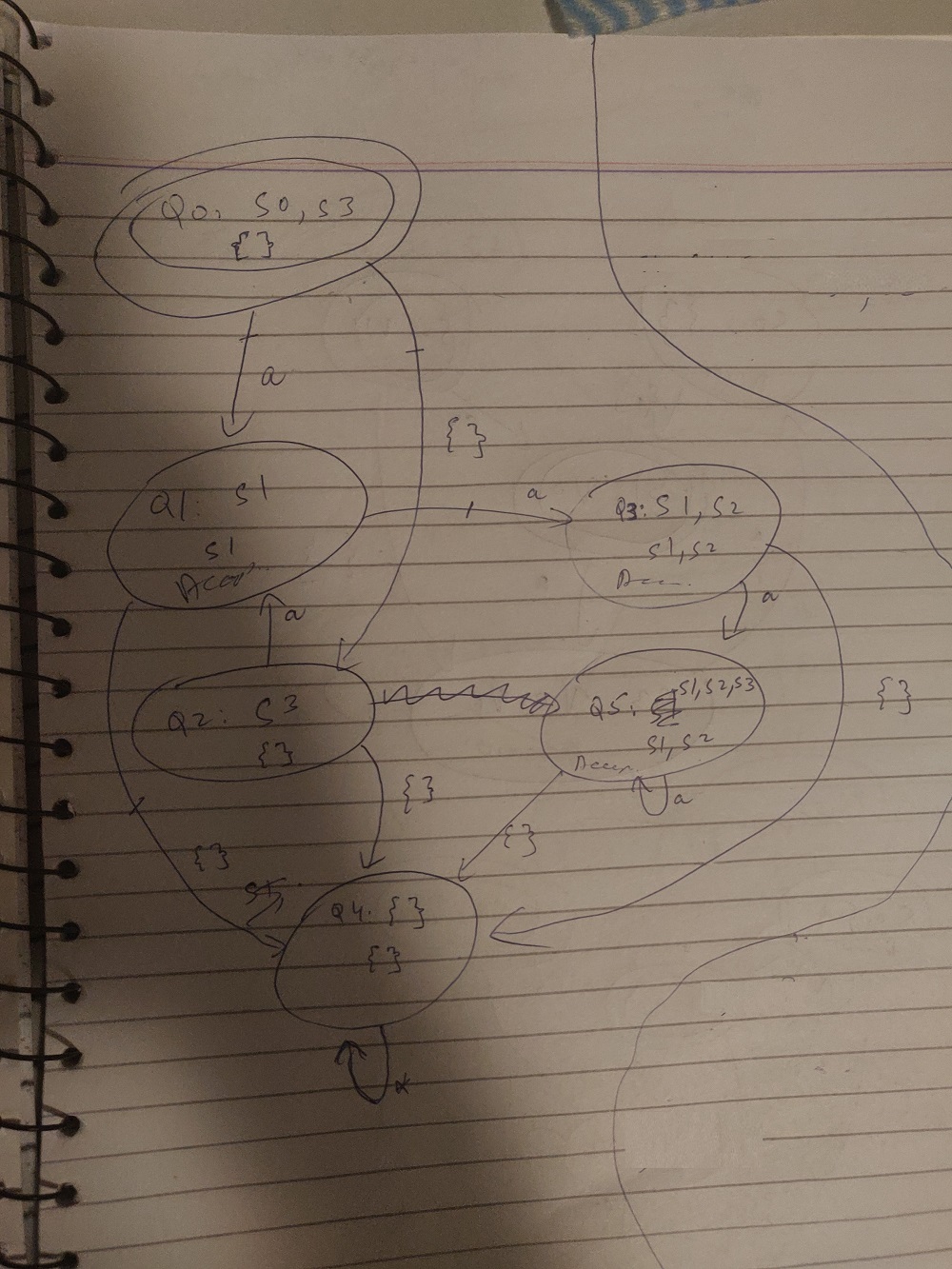
My answer for this was

labels 0:s0,s3; 1:s1; 2:s3; 3:s1,s2; 4:; 5:s1,s2,s3;     // encode Q

labels 0:; 1:s1; 2:; 3:s1,s2; 4:; 5:s1,s2;     // encode Qf

init 0;

transitions (0,{a},,1); (0,{},,2); (1,{a},,3); (1,{},,4); (2,{a},,1); (2,{},,4); (3,{a},,5); (3,{},,4); (5,{a},,5); (5,{},,4); (4,{a},,4); (4,{},,4);

accept 1,3,5;

This answer was accepted.

My question is related to type of automaton.

G: Safety Automata: it means always in accepting state.

F: Liveness Automata: it means eventually visit an accepting state at least once.

FG: Co-Büchi Automata: always visit an accepting state.

GF: Büchi Automata: final state must be accepting state.

 
If I am given just an automaton like the one, I drew in my first step. How can I determine the type of automaton from that?


Thank you in advance!

Answer 1

Great that you managed the task. 

About your question: If just an automaton is given with some accepting states, you cannot know or guess the acceptance condition. For any automaton and any set of accepting states, you could consider anyone of the acceptance conditions G,F,GF,GF and also others. The language accepted by the automaton will typically change with the acceptance condition. We have to decide what we want to express with the automaton and based on that, we have to determine the right state transitions, initial states, accepting states, and acceptance condition. That is part of the specification that somebody has to carefully make.

Bytheway, you can also double-check your result with the teaching tool https://es.cs.uni-kl.de/tools/teaching/Automata.html when you use the following input (where a0 means {} and a1 means {a}):

inputs a0,a1;
init 0,3;
transitions
    (0,a0,3); (0,a1,1);
    (1,a1,1); (1,a1,2);
    (2,a1,3);
    (3,a1,1);
accept 1,2;

Then, the given automaton looks like this (as you know): 

and the one obtained by the breakpoint construction is as follows: 

Comments

After this point how could we decide about the type of the deterministic automaton? could you please explain?

---

Well, automata are there to accept a language, and to accept the right language you need the right acceptance condition as well as the right states and transitions. So, the language that is to be specified determines which kind of acceptance condition is required. Sometimes, we have choices, but sometime, a certain acceptance condition is required.

---

could you please give an example wrt the above diagram?

---

Hi could you please give an example wrt the above diagram?

---

Consider the automaton with states s0,s1,s2,s3 above where the accepting states are s1,s2. First examine the words that can be read from the states. From s0, words a1 a1^* and a0 a1 a1^* are read, from s1, words of the form a1^* can be read, from s2, words a1 a1 a1^* can be read, and from s3 words a1 a1^* can be read.

If the automaton would be a safety automaton, then it would not accept any word, since the initial states are already unsafe. If it would be a liveness automaton, then words a1 a1^* and a0 a1 a1^* are accepted by runs from s0, and words a1 a1^* can be accepted from s3. Hence, as a liveness automaton, the automaton accepts the words a1 a1^* and a0 a1 a1^*. If the acceptance would be a persistence condition, then the same set of words will be accepted. Hence, we can use F or FG interchangably for this automaton. The reason for this is that instead of switching from s1->s2->s3->s1 we can do instead s1->s1->s1->s1 and will not leave the accepting states.