From FSMs to Kripke Structures (exercise sheet 5 question 1.c and 1.d)

Question

a) Construct a propositional logic formula that encodes the set of initial states I′ of the Kripke structure.
b) Construct a propositional logic formula that encodes the set of reachable states S′reach of the Kripke structure.

c) R1 is obtained by removing the transitions to deadends in R′. 

d) R2 is obtained by removing the transitions from/to unreachable states in R1. 

My solutions for part a and b are correct but not for c and d! Would you please tell me what wrong I did?

Comments

Can you let us know what part a), b), c) and c) is? Clearly, I could look it up this semester, but note that next year, nobody would understand what we are talking about.

---

sure. I just edited my question. Thank you.

Answer 1

So, you have the following FSM with state variables p,q and input variable a: 

    I = !q
    R = a&p&!q&next(p)&next(q) |
        a&q&next(p)&next(q) | 
        a&!p&!q&!next(p)&!next(q)

which leads to the following Kripke structure:

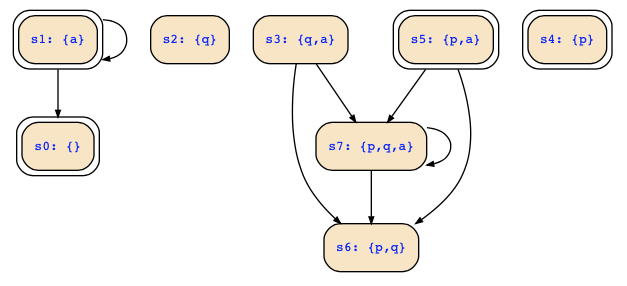
There are the following deadend states: p&q&!a | p&!q&!a | !p&q&!a | !p&!q&!a; note that one of them satisfies the initial condition. This formula can be simplified to !a, so that a transition relation that does not have transitions to deadend states would be

R' = R & next(a)

which yields as expected the following transitions

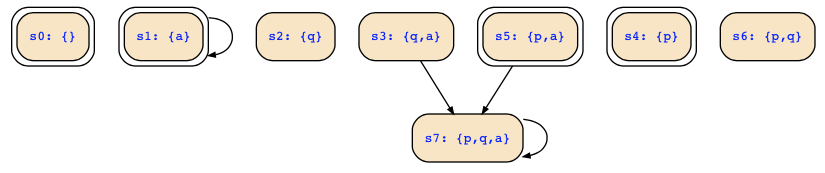
In the same way you can eliminate the transition from s3 (an unreachable state).

Comments

That's already the deadends in the question.

Note: The task is to update the transition relation R, not to give a set of states.

---

regarding this, for part c my solution is:
(a&!p&!q&!next(p)&!next(q)) | (p&a&!q&next(p)&next(q)) | (q&a&!p&next(p)&next(q)) | ( p&q&a&next(p)&next(q))

and for part d:
(a&!p&!q&!next(p)&!next(q)) | (p&a&!q&next(p)&next(q)) | ( p&q&a&next(p)&next(q))

but non of them is correct. What is the problem with my solution?

---

If I see that correctly, you have not made any change to the transition relation in part c), you just computed a full DNF as

        a & !p & !q & !next(p) & !next(q) |
        a &  p & !q &  next(p) &  next(q) |
        a & !p &  q &  next(p) &  next(q) |  
        a &  p &  q &  next(p) &  next(q)

However, in part c) you should remove transitions leading to deadend states. As I wrote, that should change the transition relation to R1 = R & next(a) which is
        a &  p & !q &  next(p) &  next(q) & next(a) |
        a &       q &  next(p) &  next(q) & next(a) |
        a & !p & !q & !next(p) & !next(q) & next(a)

The two formulas are not the same. Mine removes transitions where variable "a" holds in the target state while yours has done no changes.